 |
UNIVERSIDAD PILOTO DE COLOMBIA SECCIONAL ALTO MAGDALENA GIRARDOT |
||||||||||||||||||
       |
|||||||||||||||||||
|
NOTACIÓN SINTOTICA Un algoritmo es una secuencia de pasos con ciertas Características:
Un algoritmo será mas eficiente comparado con otro, siempre que consuma menos recursos, como el tiempo y espacio de memoria necesarios para ejecutarlos. La eficiencia de un algoritmo se puede medir:
ASINTOTAS Análisis de la eficiencia algorítmica nos lleva a estudiar el comportamiento de los algoritmos frente a condiciones extremas. Matemáticamente hablando cuando N tiende al infinito , es un comportamiento asintótico.
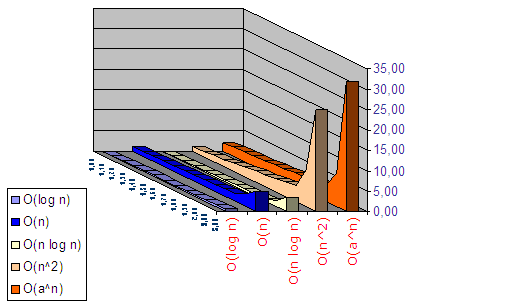
ORDEN DE COMPLEJIDAD Las funciones de complejidad algorítmica más habituales en las cuales el único factor del que dependen es el tamaño de la muestra de entrada n, ordenadas de mayor a menor eficiencia son:
REGLAS DE LA NOTACIÓN ASINTOTICA
REGLA DE LA SUMAUMA:
Se puede decir que:
T1(n) + T2(n) =O(max(f1(n),f2(n))
REGLA DEL PRODUCTO
Se puede decir que:
T1(n) T2(n) = O(f1(n) f2(n)
ESTIMACIÓN DE LA COMPLEJIDAD EN LA NOTACIÒN ASINTÒTICA
ASIGNACIONES Y EXPRESIONES SIMPLES (=)
El tiempo de ejecución de toda instrucción de asignación simple, de la evaluación de una expresión formada por términos simples o de toda constante es O(1). SECUENCIAS DE INSTRUCCIONES (;) El tiempo de ejecución de una secuencia de instrucciones es igual a la suma de sus tiempos de ejecución individuales. T(S1 ; S2) = T(S1) + T(S2) Aplicando la regla de la suma: O(T(S1 ; S2)) = max(O( T(S1), T(S2) ))
INSTRUCCIONES CONDICIONALES (IF, SWITCH-CASE) El tiempo de ejecución para una instrucción condicional IF-THEN es el tiempo necesario para evaluar la condición, más el requerido para el conjunto de instrucciones que se ejecutan cuando se cumple la condición lógica. T(IF-THEN) = T(condición) + T(rama THEN) Aplicando la regla de la suma: O(T(IF-THEN)) = max(O( T(condición), T(rama THEN) ))
El tiempo de ejecución de un condicional múltiple (SWITCH-CASE) es
el tiempo necesario para evaluar la condición, más el mayor de los
tiempos de las secuencias a ejecutar en cada valor condicional.
Ejemplo :
halla el factorial de un número n cualquiera.
int factorial(int n) O(1) { int fact = 1; O(1) for(int i = n; i > 0; i--) O(n) fact = fact * i; O(1) return fact; O(1) }
Los algoritmos usuales para la suma de matrices cuadradas de
Dimensión
n£n
requieren realizar
n2
sumas. Si se trata de un producto de matrices, es preciso
multiplicar escalar mente cada fila del primer factor por cada
columna del segundo. Un producto escalar de un vector de
n
elementos exige
n
multiplicaciones y
n
¡ 1 sumas, de forma que el tiempo de ejecución de una multiplicación
de dos matrices
n
£
n
es el requerido para
n2
sumas y
n3
¡
n2
multiplicaciones. La multiplicación suele Dominar en coste a la
suma, y está claro que, para matrices de un tamaño moderado, el
sumando
n2
es despreciable respecto a
n3.
De esta forma, adquiere sentido la afirmación “el producto de
matrices consume un tiempo proporcional a
n3”.
|
|||||||||||||||||||
Jose Said Uricoechea Sandoval - Jose Roberto Reyes - Elkin Espinosa Ingenieria de Sistemas VI Semestre |
|||||||||||||||||||
