ARBOLES

En cuanto a la posición dentro del árbol:

Nodo raíz

Nodo hoja

Nodo rama

 

En relación a su tamaño:

Orden

Grado

Nivel

Altura

 

 

 

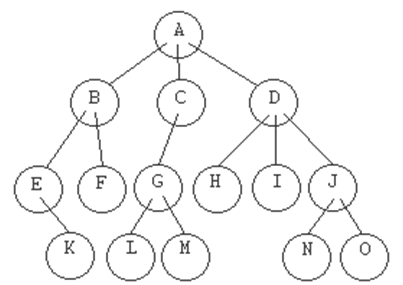
NODO PADRE

 

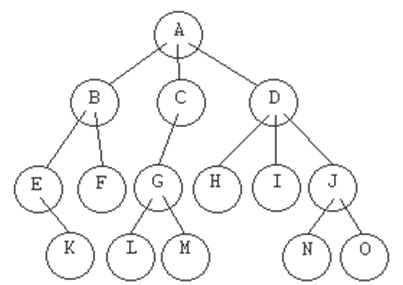
Nodo que contiene un puntero al nodo actual. En el ejemplo, el nodo 'A' es padre de 'B', 'C' y 'D'.

 

 

 

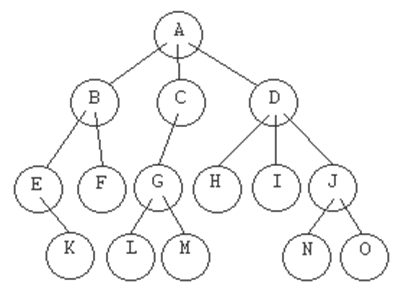
NODO RAIZ

 

Nodo raíz: nodo que no tiene padre. Este es el nodo que usaremos para referirnos al árbol. En el ejemplo, ese nodo es el 'A'.

 

 

 

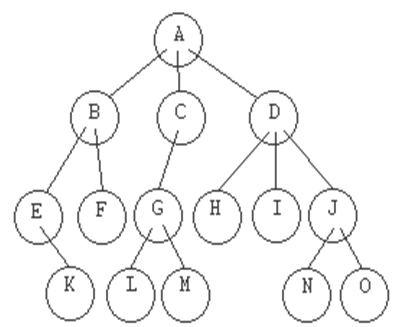
NODO HOJA

 

Nodo que no tiene hijos. En el ejemplo hay varios: 'F', 'H', 'I', 'K', 'L', 'M', 'N' y 'O'.

 

 

 

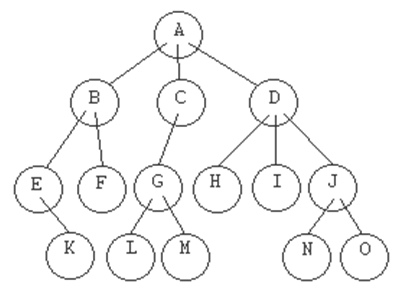
NODO RAMA

 

Estos son los nodos que no pertenecen a ninguna de las dos categorías anteriores. En el ejemplo: 'B', 'C', 'D', 'E', 'G' y 'J'.

 

 

 

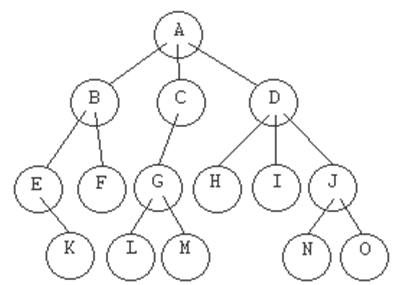
ORDEN

 

Es el número potencial de hijos que puede tener cada elemento de árbol.

 

El árbol es de 3 orden.

 

 

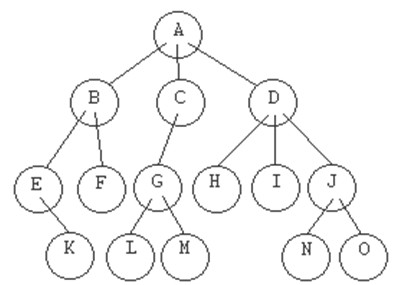
GRADO

 

El número de hijos que tiene el elemento con más hijos dentro del árbol. En el árbol del ejemplo, el grado es tres, ya que tanto 'A' como 'D' tienen tres hijos.

 

 

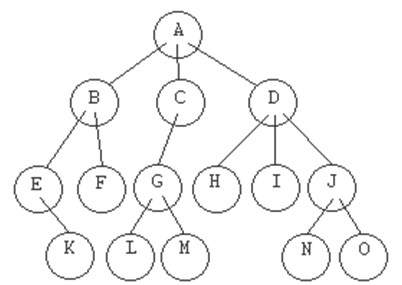
NIVEL

 

Se define para cada elemento del árbol como la distancia a la raíz, medida en nodos. El nivel de la raíz es cero y el de sus hijos uno. Así sucesivamente. En el ejemplo, el nodo 'D' tiene nivel 1, el nodo 'G' tiene nivel 2, y el nodo 'N', nivel 3.

 

 

ALTURA

 

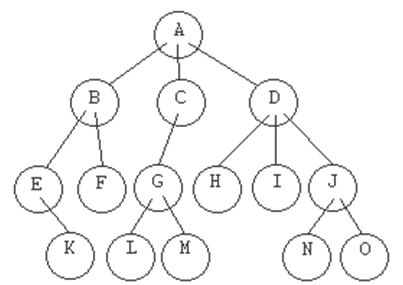
Se define como el nivel del nodo de mayor nivel. Como cada nodo de un árbol puede considerarse a su vez como la raíz de un árbol, también podemos hablar de altura de ramas. El árbol del ejemplo tiene altura 3, la rama 'B' tiene altura 2, la rama 'G' tiene altura 1, la 'H' cero.

 

 

RECORRIDOS POR UN ARBOL

 

Hay tres formas de recorrer un árbol, y las tres se suelen implementar mediante recursividad. En los tres casos se sigue siempre a partir de cada nodo todas las ramas una por una, los recorridos son:

 

Pre-orden

In-orden

Post-orden

 

Pre-orden (R.I.D)

A B E K F C G L M D H I J N O

 

In-orden (D.R.I)

K E B F A L G M C H D I N J O

 

Post-orden (I.D.R)

K E F B L M G C H I N O J D A

ARBOLES ORDENADOS

 

Un árbol ordenado, en general, es aquel a partir del cual se puede obtener una secuencia ordenada siguiendo uno de los recorridos posibles del árbol: inorden, preorden o postorden.

 

Existen varios tipos de árboles ordenados:

 

Árboles ABB

Árboles AVL

 

Árboles Binarios de Búsqueda (ABB):

 

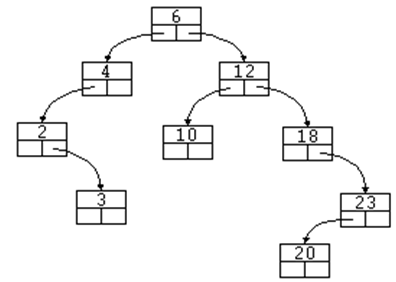
Se trata de árboles de orden 2 en los que se cumple que para cada nodo, el valor de la clave de la raíz del subárbol izquierdo es menor que el valor de la clave del nodo y que el valor de la clave raíz del subárbol derecho es mayor que el valor de la clave del nodo.

 

 

ARBOLES DEGENERADOS

 

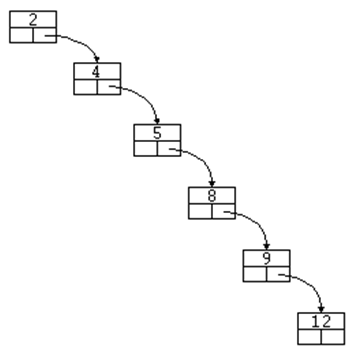
Los árboles binarios de búsqueda tienen un gran inconveniente. Por ejemplo, supongamos que creamos un ABB a partir de una lista de valores ordenada:

2, 4, 5, 8, 9, 12 Difícilmente podremos llamar a la estructura resultante un árbol:

 

 

ARBOLES AVL

 

(llamado así por las iniciales de sus inventores: Adelson - Velskii y Landis) es un árbol binario de búsqueda en el que para cada nodo, las alturas de sus subárboles izquierdo y derecho no difieren en más de 1.

 

FACTOR DE EQUILIBRIO

 

El factor de equilibrio es la diferencia entre las alturas del árbol derecho y el izquierdo:

 

FE = altura subárbol derecho - altura subárbol izquierdo;

 

Para un árbol AVL, este valor debe ser -1, 0 ó 1.

 

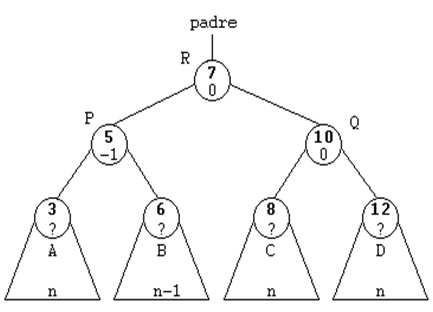
ROTACIONES DE NODOS

 

Cuando un árbol no cumple la propiedad avl se procede a realizar rotación para que se equilibre o bien para que cumpla que sea árbol avl existen 4 rotaciones:

 

Rotación simple a la derecha (SD)

Rotación simple a la izquierda (SI)

Rotación doble a la derecha (DD)

Rotación doble a la izquierda (DI)

 

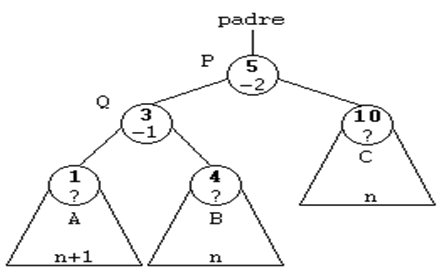
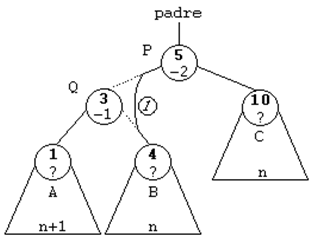
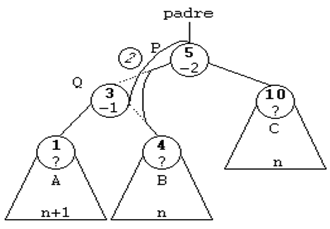
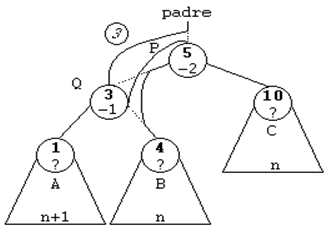
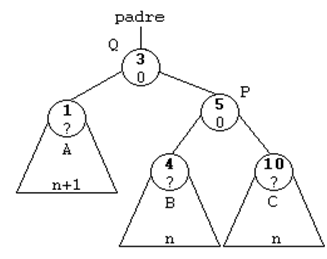
ROTACION SIMPLE A LA DERECHA (SD)

 

Esta rotación se usará cuando el subárbol izquierdo de un nodo sea 2 unidades más alto que el derecho, es decir, cuando su FE sea de -2. Y además, la raíz del subárbol izquierdo tenga una FE de -1, es decir, que esté cargado a la izquierda.

 

 

 

 

 

 

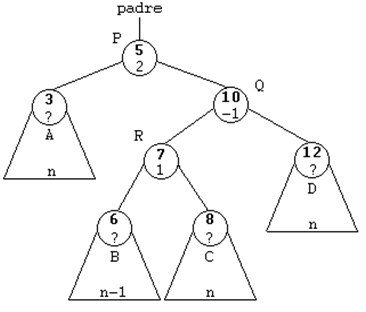
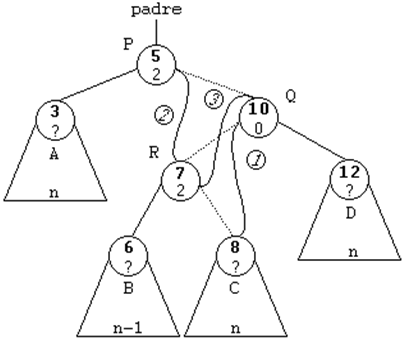
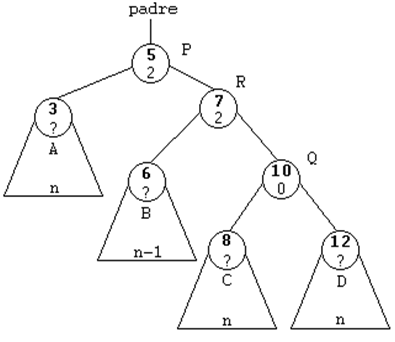
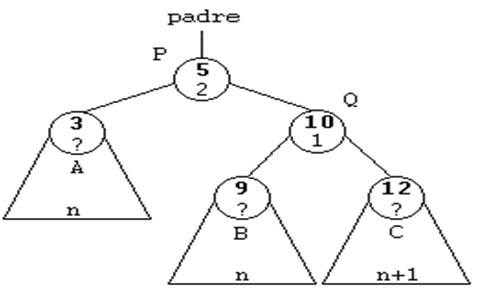
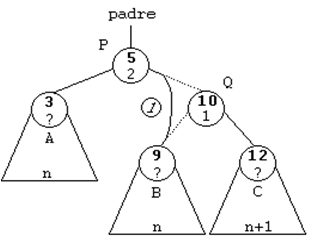
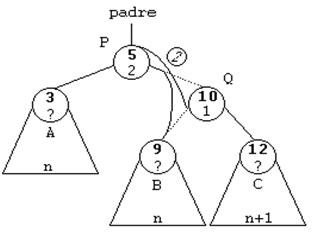
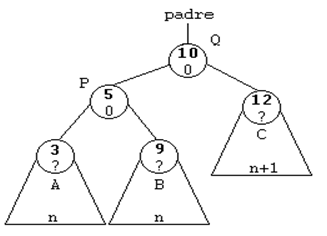
ROTACION SIMPLE A LA IZQUIERDA (SI)

 

Se trata del caso simétrico del anterior. Esta rotación se usará cuando el subárbol derecho de un nodo sea 2 unidades más alto que el izquierdo, es decir, cuando su FE sea de 2. Y además, la raíz del subárbol derecho tenga una FE de 1, es decir, que esté cargado a la derecha.

 

 

 

 

 

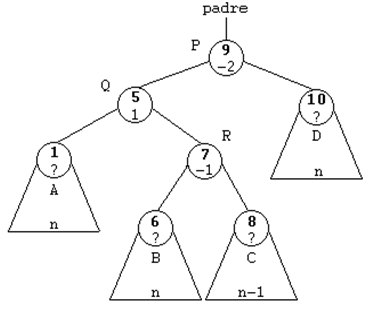
ROTACION DOBLE A LA DERECHA (DD)

 

Esta rotación se usará cuando el subárbol izquierdo de un nodo sea 2 unidades más alto que el derecho, es decir, cuando su FE sea de -2. Y además, la raíz del subárbol izquierdo tenga una FE de 1, es decir, que esté cargado a la derecha.

 

 

 

 

 

 

 

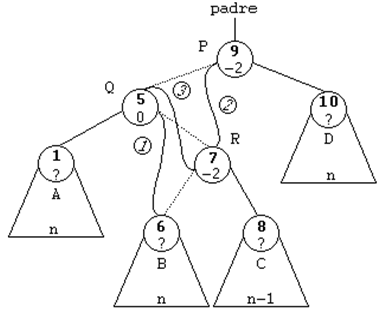
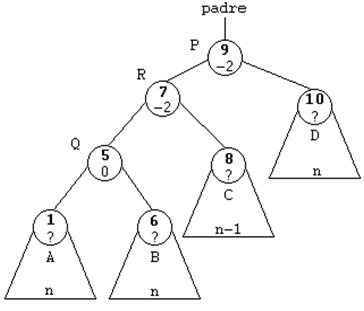
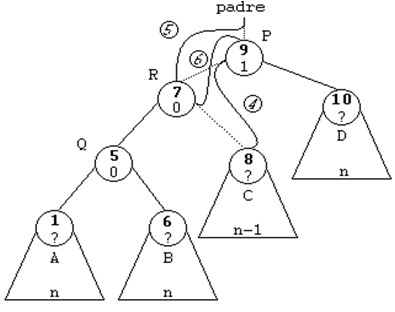
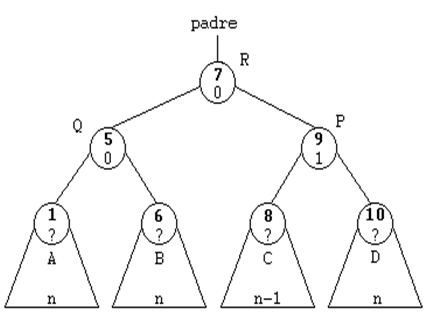
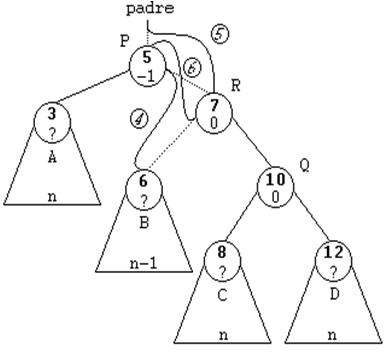
ROTACION DOBLE A LA IZQUIERDA (DI)

 

Esta rotación se usará cuando el subárbol derecho de un nodo sea 2 unidades más alto que el izquierdo, es decir, cuando su FE sea de 2. Y además, la raíz del subárbol derecho tenga una FE de -1, es decir, que esté cargado a la izquierda. Se trata del caso simétrico del anterior.